
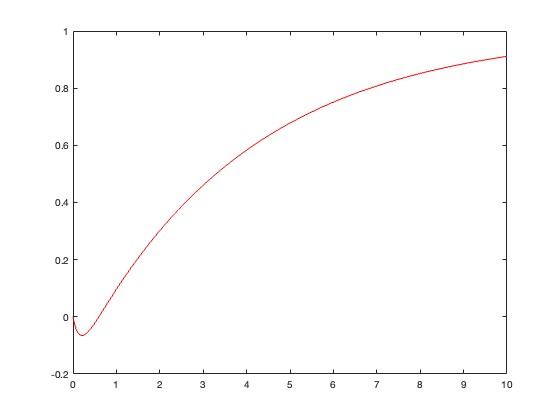
我们对系统降阶之后,其对应的波形在0点附近会先下降出现负值再回来,类似临界阻尼中峰值会超过1.
 7 X4 N2 e5 E- |& G* k; | k* {
7 X4 N2 e5 E- |& G* k; | k* {可梦之 发表于 2024-3-17 19:36
万分感谢!
6 I F/ i" g7 m6 T
正定函数这个,书上证明系统是passive的时候用到了,不过理论证明太抽象,认怂跳过去了。你这 ...
晨枫 发表于 2024-3-18 09:54$ |0 i% J1 ^3 [3 x
梦兄太客气。1 ~! I" X5 W( l) d
6 B p2 e" s' o: _
这个好像是non-minimum phase的样子,你是不是降阶后产生一个右半平面的零点?应该就是这 ...
| 欢迎光临 爱吱声 (http://aswetalk.net/bbs/) | Powered by Discuz! X3.2 |