 0 _5 t) C) N1 m1 I3 u
0 _5 t) C) N1 m1 I3 u
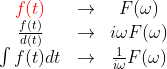
 ! k# i2 i S, l' X3 C9 }( t6 [9 P" l
! k# i2 i S, l' X3 C9 }( t6 [9 P" l
 ! ]/ Z2 m' O) w
! ]/ Z2 m' O) w
数值分析 发表于 2023-9-27 12:05
高斯小时候提出的 只是等差数列求和公式吧?

数值分析 发表于 2023-9-28 04:40 `( d0 e# B8 v/ X
又看了一遍,时域变频域的好处似乎应该加上卷积变乘法,在电路里输入卷积上冲激响应等于输出实在是太好用了 ...

| 欢迎光临 爱吱声 (http://aswetalk.net/bbs/) | Powered by Discuz! X3.2 |